手写数字识别-Kernel Support Vector Machine-论文翻译-毕设系列
写在前面的话
- 本篇博文是翻译自Code Project上的César de Souza教授的关于用Kernel Support Vector Machine手写数字识别的博客。认真学习借鉴一下。
- 出处:Handwriting Recognition Revisited: Kernel Support Vector Machines
博文正文
- 在上一篇文章中,我们讨论了怎么利用基于核函数的辨别分析(Kernel Discriminant Analysis)的方法来解决手写数字识别的问题。在这里,我们将要讨论如何利用基于核函数的支持向量机(Kernel Support Vector Machine)的一些技巧来解决手写数字的识别问题。
 Download source code - 584 KB
Download source code - 584 KB  Download sample application - 522 KB
Download sample application - 522 KB Download the Accord.NET Machine Learning Framework.
Download the Accord.NET Machine Learning Framework.- 由于在最新的代码库中,它通常包含了最新的功能增强和修正,所以请下载 最新的Accord.NET Framework.
简介
- 在上一篇文章中,我想向大家展示怎么用核判别分析法来解决手写数字识别的问题。但是,我发现自己并没有更多的关注手写数字识别的问题,因为我把焦点都放在了KDA方法上了,而不是识别问题本身。在本篇文章中,我会给大家展示一个更好的方法来解决数字识别的问题。
- 核判别分析方法有自己的问题集。尽管它在处理高维度的数据是没有任何问题,但当样本的数量达到O(n³),它就显得有些无能为力了。另外一个更严重的问题是在模型评估过程中核判别分析方法需要载入全部数据集,这样令它很难推广(例如嵌入式系统)。
- 在上一篇文章的最后,我提到了SVM其实是一种解决数字识别的更好的方法。SVM的一个优点是它们的解决问题的方法比较单一,不像KDA,它们在数据评估的过程中不需要载入全部数据集,而只是需要非常小部分的数据。这部分数据就是我们所通常称的”支持向量”。
支持向量机
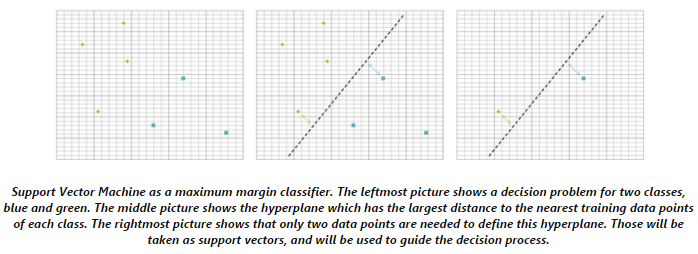
- 支持向量机是属于监督学习方法中的一种,它既可以用作分类,也可以用做回归。简单的说,给定一个训练数据样本,其中的每条记录都有一个标记变量,它标记着本条记录是属于哪一个分类的(现在讨论的是二类分类器),然后数据集通过SVM分类器进行训练得到一个决策模型,这个模型可以预测新进来的一条记录是属于两个分类中的哪一种。如果样本中的每条记录是落在空间上的某个点,那么一个SVM的线性分类器可以看做是空间中的一个分界,把空间分成两类,这样我们希望把样本分成两类的清晰的间隔,它越宽越好。新的样本点看它落在间隔的那一边上就可以预测它属于那一类的了。
- 一个线性SVM是由给定的支持向量z集合和权重w集合组成。由N个支持向量z1,z2…zN和w1,w2…wN构成的支持向量机输出的计算公式是:
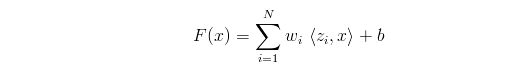
- 一个决策函数通常把这个作为输入变量,然后转化为一个二类分类器。通常地,我们用sign(.)函数,就是符号函数,输入变量大于0的作为一类,输入变量小于0的作为另外一类。
基于核函数的支持向量机
- 如上所述,原始的SVM的最优化平面是一个线性分类器。然而,从它在1963年提出的30年后,一些研究者(包括原提出者自己)建议把核技巧应用到那些最大边界超平面来创建一个非线性分类器。结果引起了研究“核方法”的一片浪潮,而核方法开始成为一个最有力的而且最受欢迎的分类方法。
- 不容置疑的是,核技巧是一种非常有力的工具,它提供了一种仅仅依赖于求两个向量的点积的算法来打通了线性和非线性的之间的桥梁。事实上,我们首先把输入数据映射到一个高维空间,然后一个线性的算法就可以在这个空间上操作在原始空间中的非线性的输入数据。
- 这个“技巧”的厉害之处在于它根本就不用计算映射后的点积;我们所需要做的是找到一个适合的核函数来代替所有的点积(这样便可以简化了计算)。核函数标记特征空间中的一个内积,它通常记为:
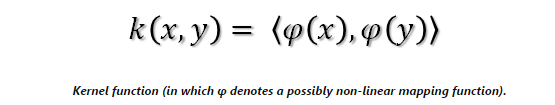
(其中Ψ()代表映射函数)。 - 利用核函数,算法能被带入到高维空间而不需要明确的把输入点映射到这个空间上。这是非常取巧的,特别是当高维的特征空间是无穷多维的,它是不可以计算的时候。正是由于原始的SVM的公式中包含点积运算,它是可以直接应用核技巧的。即使结果分类器在高维特征空间中是个超平面,但在原始空间中它还是非线性的。核技巧的应用同样为不同的视野去进行比较的分类器提供了非常有力的理论支持,例如,生物。

- 可以很明显的看出,通过核函数(of the form K(z,x) = <z,x> = zTx),我们又得到了原始线性SVM的相似公式。想了解更详细的关于核技巧的资料和核函数应用的例子,可以参考previous article about Kernel Discriminant Analysis,或者Kernel Functions for Machine Learning Applications。
多分类的支持向量机
- 很不幸的,不像KDA,支持向量机并没有很自然的推广到多分类的问题。原始的SVM是一个二类分类器,它一次只可以在两个分类中进行预测。然而,现实问题需要更多的是可以用SVM解决多分类问题,下面我们就来举一个例子。
- 假设我们有三个分类A,B,C。现在,假设我们只有二类分类器,那么我们怎么把二类分类器去解决一个多分类器的问题呢?其中一个可行的方法就是把我们的多分类问问题拆成多个二类分类器的集合。下面左边的矩阵是泳衣解决三个分类的分类器的二类分类器的所有组合:

- 然而,注意到上面左边的矩阵中有一些多余的情况。譬如,计算AxA是没有意义的。还有,计算AxB之后再计算BxA是很低效率的,我们计算了AxB后,可以通过取反就得到了BxA。丢弃了多余的选项后,我们只剩下右边的(半透明的,除了AxA,BxB,CxC)矩阵。观察可知,一个n类的分类问题可以拆分成n(n-1)/2个二类分类器的组合组成的小的子集合。
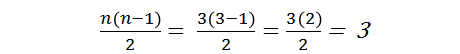
- 现在我们得到了3个二类分类的问题,所以,我们需要创建3个SVM来解决每一个子问题。

- 要确定一个分类,我们就看3个SVM当中谁的投票最多。譬如,A在第一个SVM中胜出,而C在其他的两个SVM中都胜出。

- 如果我们把胜出次数最多的作为赢家,那么我们应该把它归为C类。这种方法通常称作多分类器中的”一对一”策略。

- 另外一种方法是利用“一对多”的策略,把输入放到所有的SVM中,然后选择最高的输出的那个SVM。很不幸的,我们不能保证有最高的输出就是最好的SVM。这个不作本文讨论的范畴。
源代码
- 基于核方法的支持向量机的代码也是属于Accord.NET的一部分,这个框架我做了数年。它是在AForge.NET的顶层建立的,AForge.NET是计算机视觉,机器学习中非常受欢迎的框架,它集合了我过去的研究中的多个主题。目前,它有了PCA, KPCA, LDA, KDA, LR, PLS, SVMs, HMMs, LM-ANN和其他的缩写。这个项目在Github上举办,地址是:https://github.com/accord-net/framework/。最小的版本中包含了最小的bug修正,完善和功能加强,新特征等,我强烈推荐大家直接从Github上下载最新的版本库。
支持向量机
- 支持向量机类结构如下:(C#和VB实现)
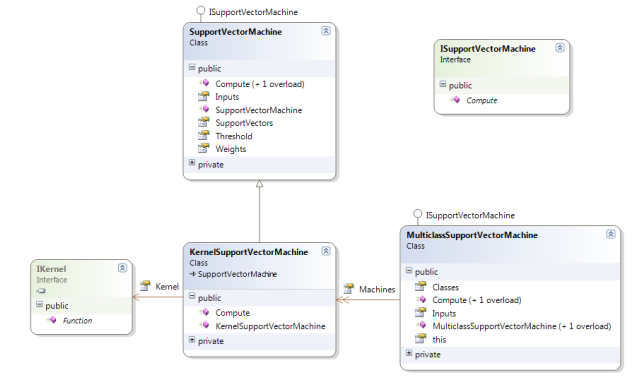
- KernelSupportVectorMachine类继承SupportVectorMachine类,加了kernel方法。MulticlassSupportVectorMachine类集合了一堆实现了“一对一”策略的KernelSupportVectorMachines类来实现多分类器。框架的API在此:extensive list of machine learning kernel functions to chose from.
训练算法
- 训练算法既可以实现分类也可以实现回归。它们是Platt的序列最优化(SMO)算法的直接实现。MulticlassSupportVectorLearning类提供了一个回调函数,名字是Configure,它可以被任何的算法选择并进行配置。这个方法并没有强加需要利用哪一种算法,而且还允许用户利用自定义的算法来进行训练。

- 因为MulticlassSupportVectorLearning算法一次可以训练一堆独立的机器,所以它容易实现并行运算。事实上,这些实现方法在单台机器中可以充分利用剩下的核。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27/// <summary>
/// Runs the one-against-one learning algorithm.
/// </summary>
public double Run(bool computeError)
{
// For each class i
AForge.Parallel.For(0, msvm.Classes, delegate(int i)
{
// For each class j
for (int j = 0; j < i; j++)
{
// Retrieve the associated machine
var machine = msvm[i,j];
// Retrieve the associated classes
int[] idx = outputs.Find(x => x == i || x == j);
double[][] subInputs = inputs.Submatrix(idx);
int[] subOutputs = outputs.Submatrix(idx);
// Transform in a two-class problem
subOutputs.ApplyInPlace(x => x = (x == i) ? -1 : 1);
// Train the machine on the two-class problem.
configure(machine, subInputs, subOutputs).Run(false);
}
});
} - 上面的代码利用了AForge.NET Parallel的构造器和Accord.NET matrix extensions。我决定不用最新加的 .NET 4.0 Parallel Extensions,所以这个框架还是兼容.NET 3.5 applications的应用的。
数字识别
UCI的光学数字数据集
- 如果你读了上一篇文章Kernel Discriminant Analysis for Handwritten Digit Recognition,那么请跳过本小节。本小节只是对UCI机器学习的光学数字数据库的介绍。
- UCI机器学习库是一个被机器学习社区用于做机器学习算法实践分析的数据库,域理论,数据生成器的集合。其中一个就是光学识别的手写数字数据集,又叫Optdigits Dataset.
- 原始的光学数字数据是一个个32x32的矩阵。它们提供经过预处理的数字形式,数字被分成非重叠的4x4块,每一块上像素都合计了。这就生成了8x8输入矩阵,每一个元素都是0到16的整数。

基于多分类的SVM的数字分类器
- 核方法引起了很大的兴趣,因为它可以应用到那些需要进行预处理的(例如,数据降维)数据的问题上和被模型化的数据结构的扩展知识上。即使我们对数据知之甚少,核方法的直接应用往往得到令人感兴趣的结果。利用核方法实现最佳化是一个非常难的任务,因为我们用无穷多的核函数可供选择,而每个核函数也有无穷多的参数可供调整。
- 下面的代码向我们展示了基于核函数的支持向量机是怎么实现的。输入的是一个1024的全向量。这个对神经网络来说是不切实际的,例如,通常的核方法处理高维数的问题是没问题的,因为它不会遭受维数灾难。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36// Extract inputs and outputs
int samples = 500;
double[][] input = new double[samples][];
int[] output = new int[samples];
for (int i = 0; i < samples; i++)
{
...
}
// Create the chosen Kernel with given parameters
IKernel kernel = new Polynomial((int)numDegree.Value, (double)numConstant.Value);
// Create the Multi-class Support Vector Machine using the selected Kernel
ksvm = new MulticlassSupportVectorMachine(1024, kernel, 10);
// Create the learning algorithm using the machine and the training data
var ml = new MulticlassSupportVectorLearning(ksvm, input, output);
// Extract training parameters from the interface
double complexity = (double)numComplexity.Value;
double epsilon = (double)numEpsilon.Value;
double tolerance = (double)numTolerance.Value;
// Configure the learning algorithm
ml.Configure = delegate(KernelSupportVectorMachine svm,
double[][] cinput, int[] coutput)
{
var smo = new SequentialMinimalOptimization(svm, cinput, coutput);
smo.Complexity = complexity;
smo.Epsilon = epsilon;
smo.Tolerance = tolerance;
return smo;
};
// Train the machines. It should take a while.
double error = ml.Run();
应用例子
学习
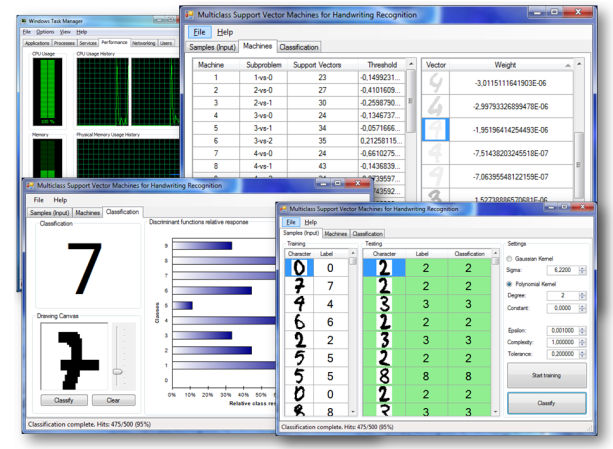
- 样例应用附带源代码,它实现了基于核函数的多分类支持向量机的手写数字识别。下载了应用后,打开并点击菜单,然后选择”Open”。它就会载入数据。
- 要开始训练数据,点击“Start training”。利用默认设置,应该不会太长时间。因为代码是用了并行运算,核数越多,训练越快。
- 训练完成后,点击“Classify”开始分类测试数据集。利用默认值,它应该可以得到95%的正确率,大概是500个数据中有475个分类正确。识别率的大小会随着每次训练的不同而有小小的波动。
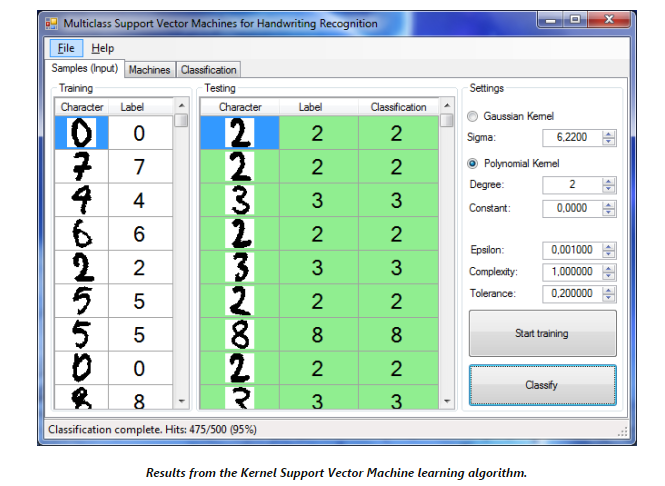
- 相同的集合和相同的训练和测试样本已经在上一篇中的基于核方法的判别分析方法中使用。而SVM却得到更高的运行效率和更少的内存,更多的样本数可能得到更高的正确率。
- 训练后,创建的SVM可以在“Machine”这个tab中看到。每次的SVM的支持向量和临界值可以在第一个数据格视图中通过选择一个数据入口而看到。向量越暗,在决策过程中它的权值就越大。
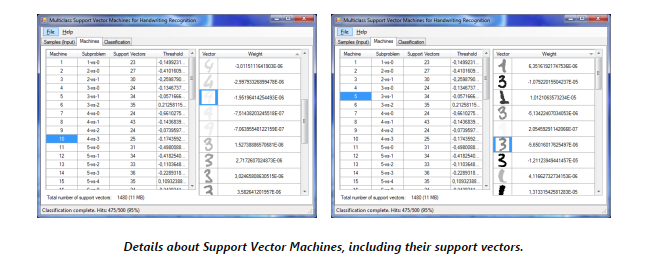
结果
- 即使识别率刚刚超过3%,但是识别的正确率已经比KDA大大的提升了。点击“Classification”tab,我们可以手动地为用户手写的数字测试多分类支持向量机。
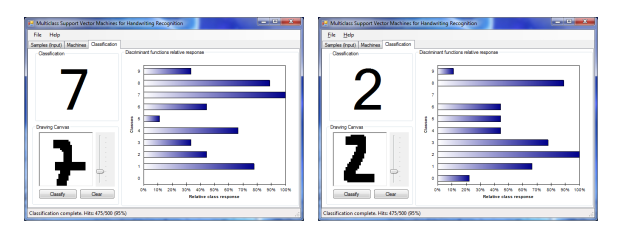
- 我们看到SVM方法产生了更强壮的结果,即使手写很差的数字也能识别正确:

- 最后,有一个视频演示:
总结
- 在本文中,我们详细叙述和探索了基于核方法的SVM来解决手写数字识别的问题,并且可以得到更好的结果。
- SVM适合小样本的数据训练。
继续阅读
- Handwriting Recognition using Kernel Discriminant Analysis
- Kernel Functions for Machine Learning Applications
- Kernel Support Vector Machines (SVM)
- Principal Component Analysis (PCA)
- Kernel Principal Component Analysis (KPCA)
- Linear Discriminant Analysis (LDA)
- Non-Linear Discriminant Analysis with Kernels (KDA)
- Logistic Regression Analysis
参考
- Wikipedia contributors,“Sequential Minimal Optimization”, Wikipedia, The Free Encyclopedia,http://en.wikipedia.org/wiki/Sequential_Minimal_Optimization (accessed April 24, 2010).
- Wikipedia contributors, “Support Vector Machine”, Wikipedia, The Free Encyclopedia,http://en.wikipedia.org/wiki/Support_vector_machine,(accessed April 24, 2010).
- John C. Platt,Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines , Microsoft Research, 1998.
- J. P. Lewis,A Short SVM (Support Vector Machine) Tutorial.,CGIT Lab / IMSC, University of Southern California.
- A. J. Smola and B. Scholkopf,A Tutorial on Support Vector Regression.,NeuroCOLT2 Technical Report Series, 1998.
- S. K. Shevade et al.Improvements to SMO Algorithm for SVM Regression,1999.
- G. W. Flake, S. LawrenceEfficient SVM Regression Training with SMO
- A. Asuncion & D.J. Newman,UCI Machine Learning Repository.Irvine, CA: University of California, School of Information and Computer Science (2007).
- Andrew Kirillov,The AForge.NET Framework.The AForge.NET Computer Vision, Artificial Intelligence and Robotics Website, 2010.
- C. R. Souza, Kernel Functions for Machine Learning Applications. 17 Mar. 2010. Web.
后记
- 翻译这篇文章后,除了对翻译的难度有了更深一层的认知之后,本次只要是对SVM进行多分类问题的解决有了更深的认识。SVM本来是一个二类分类器,那么要解决多分类问题,应该要什么思路呢?就是用二类分类器进行组合,然后通过“一对一”策略来解决多分类分类器。
- 本文标题:手写数字识别-Kernel Support Vector Machine-论文翻译-毕设系列
- 创建时间:2015-01-03 14:29:02
- 本文链接:2015/01/03/毕业设计系列/手写数字识别-Kernel-Support-Vector-Machine-博客翻译-毕设系列/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
评论