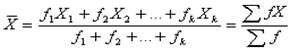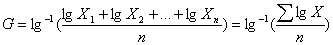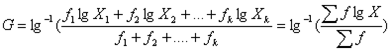概率论基本概念1

定量数据的统计特征

• 在对一组统计数据的分布变化进行深入研究之前，我们首先研究一组数据的特征。为了比较精确地描述一组统计资料的特征，需要使用一些统计指标来描述它。下面我们讨论一下数据统计特征的四个方面。

集中趋势

• 集中趋势，也称做中心位置。即表示一组数据的中心位置的数据是在什么地方，也就是数据集中分布的位置。
• 一组数据的集中趋势通常用平均数、中位数和众数等来表示。这些统计量均称为平均指标。平均指标的特点是将一组数据中各个数据之间的差异抽象化，用一个指标来代表各个数据的一般水平，它反映了一组数据中各个数据的代表水平、中心位置或集中趋势。

均数

• 均数是算术均数的简称。常用表示样本均数，表示总体均数。均数用于反映一组同质观测值的平均水平，适用于正态或近似正态分布的数值变量资料。其计算方法有：
  • 直接法
    • 用于样本含量较少时，其公式为：
    • 
    • 式中，希腊字母∑（读作sigma）表示求和；X1,X2…,Xn为观察值；n为样本含量，即观测值的个数。
  • 加权法
    • 用于频数表资料或样本中相同观察值较多时，其公式为：
    • 
    • 式中，X1,X2,…,Xn与f1,f2,…,fk分别为相同观察值与其对应的频数（或频数表资料中个组段的组中值和相应组段的频数）。

几何均数

• 适用于对数正态分布，即数据经过对数变换后呈正态分布的资料；等比级数资料，即观测值之间呈倍数或近似倍数变化的资料。如抗体滴度、平均效价等。其计算方法有：
  • 直接法
    • 适用于样本含量n较小时
    • 
      或
      
  • 加权法
    • 频数表资料或样本中相同观察值较多时
    • 
  • 注意：计算几何均数时观察值中不能有0，因为0不能取对数；一组观察值中不能同时又正值和负值。

中位数

• 一组由小到大按顺序排列的观察值中位次居中的数值。
• 中位数可用于描述：
  • 非正态分布资料（对数正态分布除外）；
  • 频数分布的一端或两端无确切数据的资料；
  • 总体分布不清楚的资料
• 在全部观察中，小于和大于中位数的观察值个数相等。其计算方法也包括：
  • 直接法
    • 适用于样本含量n较小的资料
    • 把数从小到大排成一列
    • 
  • 频数表法
    • 适用于样本含量n较大的资料
    • 

离散趋势

• 在统计学上描述观察值偏离中心位置的趋势，反映了所有观察值偏离中心的分布情况。
• 描述一组计量资料离散趋势的常用指标有极差、四分位数间距、方差、标准差、标准误差和变异系数等，其中方差和标准差最常用。

极差

• 极差(range,简记为R)亦称全距。
• 定义：值一组同质观察值中最大值和最小值之差。极差反映了个体差异的范围：极差大，说明变异度大；反之，极差小，说明变异度小。
• 公式：R = Xmax - Xmin
• 不足：
  • 1. 仅考虑了最大值和最小值之差，不能反映组内其他观察值的变异度；
  • 2. 样本含量越大，抽到较大或较小的观察值的可能性越大，故极差可能越大。因此，样本含量相差悬殊时不宜用极差比较。

平均差

• 定义：平均差是指一组数据中的各数据对平均数的离差绝对值的平均数。
• 一组数据中的各数据对平均数的离差有正有负，其和等于0，因此平均差必须用离差的绝对值来计算。
• 平均差越大，表示数据之间的变异程度越大，反之，则变异程度越小。
• 公式：

百分位数

• 定义：百分位数(percentile)用Px表示，0<x<100，是描述一组数据某百分位的位置指标。Px将全部观察值分为两部分，理论上有x%的观察值比它小，有(100-x%)的观察值比它大。

• 最常用的百分位数是P50,即中位数。

• 应用

  • 1.常与中位数结合应用，可以描述一组资料在某百分位置上的水平，也可以描述资料的分布特征。

    • 
    • M - P5 = P95 - M, 分布近似对称
    • M - P5 < P95 - M, 分布呈正偏态
    • M - P5 > P95 - M, 分布呈负偏态

  • 

  • 2.也可用多个百分位数的结合来描述一组观察值的分布特征，如P25和P75合用时，反映中间50%观察值的分布情况；

  • 3.百分位数可用于确定非正态分布资料的医学参考值范围。

• 计算公式：

  • 
  • Lx,i,fx分别为Px所在组段的下限、组距和频数；∑fL为小于L的各组段的累计频数。

• 注意：应用百分位数，样本含量要足够大，否则不宜取靠近两端的百分位数。

四分位数间距

• 定义：四分位数间距(quartile interval, Q)为上四分位数与下四分位数之差(或P75与P25之差)。
• 计算公式：
• 应用：用于描述偏态分布以及分布的一端或两端无确切数值资料或分布类型未知资料的离散程度。
• 
• 四分位数间距包括了一组观察值的一半，故可把四分位数间距看成是中间50%观察值的极差。
• 意义：Q越大，变异度越大；反之，Q越小，变异度越小。
• 特点：由于四分位数间距不受两端个别极大值或极小值的影响，因而它较极差稳定，但仍未考虑全部观察值的变异度。

方差

• 极差和四分位数间距都只考虑了个别观察值的大小差异，没有全面反映每个观察值的变异程度。
• 就总体而言，即应考虑总体中每个观察值X与总体均数μ的差值(X - μ)，即离均差。
• 因离均差之和∑(X - μ) = 0,不能反映变异度的大小，故用例均差平方和∑(X - μ)^2 (sum of squares of deviations from mean)反映之。离均差平方和的大小除与变异度有关外，还与变量值的个数N有关。为了消除这一影响，取离均差平方和的均数，称方差(variance)或均方(mean of squares)。
• 计算公式：
  • 总体方差：
  • 样本方差：
• n-1为自由度(degree of freedom),一般用ν(niu)表示。
• 因方差的度量单位是原度量单位的平方，故计算结果难以解释。

标准差

• 为了使统计量的单位同观察值单位相一致，通常将方差开平方，即得到标准差，标准差也称为均方差。
• 计算公式：
  • 总体标准差：
  • 样本标准差：
• 意义：标准差大，表示观察值的变异度大；反之，标准差小，表示观察值的变异度小。
• 应用：
  • 1. 适用于描述对称分布资料尤其是正态分布资料的离散程度；
  • 2. 结合均数，描述正态分布资料的频数分布规律，用于估计医学参考值范围；
  • 3. 结合均数，计算变异系数；
  • 4. 结合样本含量，计算标准误差，估计抽样误差，用于统计推断。

变异系数

• 变异系数(coefficient of variation, CV)，是标准差与均数的比值，用百分数表示，没有单位。
• 计算公式：
• 应用：常用于比较度量单位不同或均数相差悬殊的两组(或多组)资料的变异度。

偏度

• 定义：偏度是指次数分布非对称的偏态方向程度。为了精确测定次数分布的偏斜状况，统计上采用偏斜度指标。

峰度