问题描述与目标
描述:有害藻类的高浓度会对河流生态环境造成强大的破坏,所以对有害藻类的数量进行预测对提高河流质量有很重要的意义。
目标:影响藻类繁殖的因素有什么特征。
数据说明
本案例有2个数据集:训练集和测试集
变量说明:
名义变量
- season : 季节
- size : 河流规模
- speed : 流速
数值变量
- mxPH : 最大PH值
- mnO2 : 最小含氧量
- Cl : 平均氯化物含量
- NO3 : 平均硝酸盐含量
- NH4 : 平均氨含量
- oPO4 : 平均正磷酸盐含量
- PO4 : 平均硝酸盐含量
- Chla : 平均叶绿素含量
UCI机器学习algae数据说明链接
数据加载到R
本例直接下载”DMwR”包,然后载入R空间,就可以得到一个algae的数据框。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| > library("DMwR", lib.loc="e:/R/R-3.1.1/library")
Loading required package: lattice
Loading required package: grid
> head(algae)
season size speed mxPH mnO2 Cl NO3 NH4
1 winter small medium 8.00 9.8 60.800 6.238 578.000
2 spring small medium 8.35 8.0 57.750 1.288 370.000
3 autumn small medium 8.10 11.4 40.020 5.330 346.667
4 spring small medium 8.07 4.8 77.364 2.302 98.182
5 autumn small medium 8.06 9.0 55.350 10.416 233.700
6 winter small high 8.25 13.1 65.750 9.248 430.000
oPO4 PO4 Chla a1 a2 a3 a4 a5 a6 a7
1 105.000 170.000 50.0 0.0 0.0 0.0 0.0 34.2 8.3 0.0
2 428.750 558.750 1.3 1.4 7.6 4.8 1.9 6.7 0.0 2.1
3 125.667 187.057 15.6 3.3 53.6 1.9 0.0 0.0 0.0 9.7
4 61.182 138.700 1.4 3.1 41.0 18.9 0.0 1.4 0.0 1.4
5 58.222 97.580 10.5 9.2 2.9 7.5 0.0 7.5 4.1 1.0
6 18.250 56.667 28.4 15.1 14.6 1.4 0.0 22.5 12.6 2.9
|
- 数据框可以看做一种有列名称的矩阵或者表格,它是存储R数据表的一种理想的数据结构。函数head讲显示数据框的前6行。
数据可视化和摘要
探索性数据分析-summary
在没有充分了解数据之前,我们可以首先了解一下数据的统计特性。R中提供了一个非常便利的函数summary,下面我们从探索性数据分析着手进行分析。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| > summary(algae)
season size speed mxPH
autumn:40 large :45 high :84 Min. :5.600
spring:53 medium:84 low :33 1st Qu.:7.700
summer:45 small :71 medium:83 Median :8.060
winter:62 Mean :8.012
3rd Qu.:8.400
Max. :9.700
NA's :1
mnO2 Cl NO3
Min. : 1.500 Min. : 0.222 Min. : 0.050
1st Qu.: 7.725 1st Qu.: 10.981 1st Qu.: 1.296
Median : 9.800 Median : 32.730 Median : 2.675
Mean : 9.118 Mean : 43.636 Mean : 3.282
3rd Qu.:10.800 3rd Qu.: 57.824 3rd Qu.: 4.446
Max. :13.400 Max. :391.500 Max. :45.650
NA's :2 NA's :10 NA's :2
NH4 oPO4 PO4
Min. : 5.00 Min. : 1.00 Min. : 1.00
1st Qu.: 38.33 1st Qu.: 15.70 1st Qu.: 41.38
Median : 103.17 Median : 40.15 Median :103.29
Mean : 501.30 Mean : 73.59 Mean :137.88
3rd Qu.: 226.95 3rd Qu.: 99.33 3rd Qu.:213.75
Max. :24064.00 Max. :564.60 Max. :771.60
NA's :2 NA's :2 NA's :2
Chla a1 a2
Min. : 0.200 Min. : 0.00 Min. : 0.000
1st Qu.: 2.000 1st Qu.: 1.50 1st Qu.: 0.000
Median : 5.475 Median : 6.95 Median : 3.000
Mean : 13.971 Mean :16.92 Mean : 7.458
3rd Qu.: 18.308 3rd Qu.:24.80 3rd Qu.:11.375
Max. :110.456 Max. :89.80 Max. :72.600
NA's :12
a3 a4 a5
Min. : 0.000 Min. : 0.000 Min. : 0.000
1st Qu.: 0.000 1st Qu.: 0.000 1st Qu.: 0.000
Median : 1.550 Median : 0.000 Median : 1.900
Mean : 4.309 Mean : 1.992 Mean : 5.064
3rd Qu.: 4.925 3rd Qu.: 2.400 3rd Qu.: 7.500
Max. :42.800 Max. :44.600 Max. :44.400
a6 a7
Min. : 0.000 Min. : 0.000
1st Qu.: 0.000 1st Qu.: 0.000
Median : 0.000 Median : 1.000
Mean : 5.964 Mean : 2.495
3rd Qu.: 6.925 3rd Qu.: 2.400
Max. :77.600 Max. :31.600
|
- 由结果可知,summary的作用是:
- 名义变量(R中用因子来表示):统计数据中该变量某个值的频数。譬如,季节(season)当中秋季(autumn)出现的次数是40。
- 数值变量:summary为我们提供了均值、中位数、四分位数、极值等一系列的统计信息。譬如,最大的PH值(mxPH)当中,最小值是5.600,最大值是9.700,中位数是8.060,第一个四分位数(1st Qu),即数据排序后25%的地方,是7.700,第三个四分位数(3st Qu),即数据排序后75%的地方,是8.400,还有缺失值(NA)的个数是1.000。
数据分布状况-hist
1
| > hist(algae$mxPH, prob = T)
|
plot:

- 该指令绘制变量mxPH的直方图。设置参数pro=T,我们可以得到每个取值区间的概率,如果该参数设置为FALSE或者忽略该参数,它将给出频数。
- 由图中观察,变量mxPH的分布非常接近正态分布,它的值大部分聚集在该均值的周围。我们通过QQ图来检验该变量是否为正态分布。
1
2
3
4
5
6
7
8
| library("car", lib.loc="e:/R/R-3.1.1/library")
par(mfrow=c(1,2))
hist(algae$mxPH,prob = T, xlab='',
main="Histogram of maximun pH value", ylim=0:1)
lines(density(algae$mxPH, na.rm = T))
rug(jitter(algae$mxPH))
qqplot(algae$mxPH, main="Normal QQ plot of maximum pH")
par(mfrow=c(1,1))
|
plot:

- 左图中的曲线是平滑版本的直方图,而在X轴上密密麻麻的小直线就是变量的实际值,利用它我们可以识别出离群点。譬如,小于6的两个奇异点。
- 右图是Q-Q图,图中黑色实线是正态分布的理论分位数,而散点图就是实际变量值的描述。另外,虚线组成的区域就是符合正态分布的95%置信区间的带状图。由图可知,变量有几个小的值明显在95%的置信区间之外,它们不服从正态分布。
数据分布状况的另一种展示-箱型图
百度百科:箱型图
1
2
3
| boxplot(algae$oPO4, ylab = "Orthophosphate(oPO4)")
rug(jitter(algae$oPO4),side=2)
abline(h = mean(algae$oPO4, na.rm = T), lty = 2)
|
plot:

lattice版本的箱图-bwplot
条件绘图室依赖于某个特定因子的图形表示。因子是一个取值为有限集合的名义的变量。例如,对于变量size的不同取值,可以绘制变量a1的一组箱图。每个箱图是对应于变量size的某个特定值的水样子集。通过这些箱图可以研究名义变量size如何影响变量a1值的分布。
1
2
| library(lattice)
bwplot(size ~ a1, data = algae, ylab='River Size', xlab='Algal A1')
|
plot:
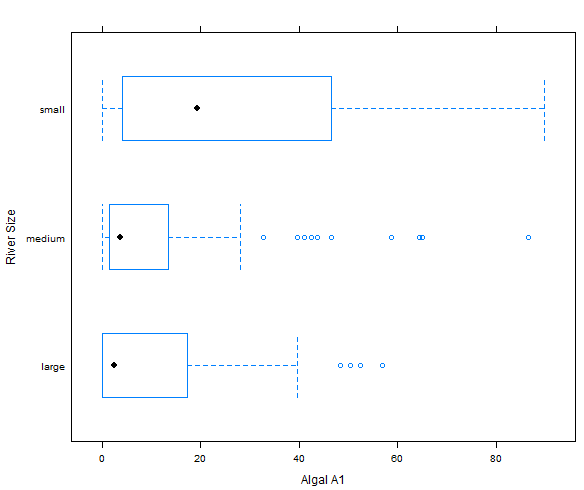
- 由上图可知,在规模较小的河流中,海藻a1的频率较高,这是很有用的信息。
Hmisc版本的箱图-bwplot
分位箱图
1
2
3
4
| library(Hmisc)
bwplot(size ~ a1, data = algae, panel = panel.bpplot,
probs=seq(.01,.49,by=.01), datadensity = TRUE,
ylab = 'River Size', xlab = 'Algal A1')
|
plot:
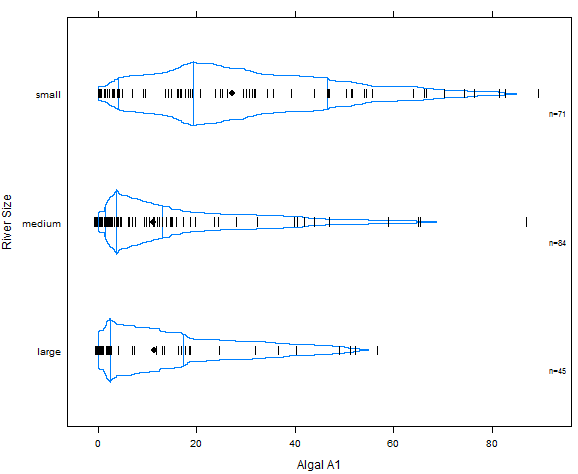
- 图中的点代表均值,而图中的竖线分别代表变量的第一个分位数、中位数和第三个分位数。图中的小竖线代表数据的真实取值,这些值的分布则由分位数图来体现。分位数箱图比上一个箱图提供了更多的信息。
- 我们可以得到以下结论:小型的河流有更高频率的海藻,但我们也观察到小型河流的海藻频率的分布比其他类型的河流频率的分布分散。
Hmisc版本的升级箱图-多个变量
这种类型的条件绘图不局限于名义变量,也不局限于单个因子。只要先把连续变量“离散化”,也同样可以进行条件绘图。下面给出一个两个因子条件绘图的例子。考虑变量a3在给定变量season和变量mnO2下的条件绘图,变量mnO2是一个连续变量,绘图代码如下所示:
1
2
3
| minO2 <- equal.count(na.omit(algae$mnO2),number=4, overlap=1/5)
stripplot(season ~ a3|minO2,
data = algae[!is.na(algae$mnO2),])
|
plot:

- 第一行调用equal.count()对连续变量mnO2离散化,把该变量转换为因子类型。参数number设置需要的区间个数,参数overlap设置两个区间之间的靠近边界的重合(这意味着某些观测值将被分配到相邻的区间中)。每个区间的观测值的个数相等。注意,变量algae$mnO2中含有NA值,所以上面的指令中没有直接应用该变量,否则会导致其后的绘图函数出错。函数na.omit()可以用来剔除向量中的任何NA值。
- 第二行调用绘图函数stripplot(),该函数是lattice包中的一个绘图函数,它根据另一个变量(这里是season)把变量的实际值绘制到不同的图形。这些区间按照从左到右,从下到上的顺序排列。即与左下方的图形相对应的是较小的mnO2值。变量mnO2中的NA值也会对图形的绘制产生影响。不能像绘制上图中那样直接应用参数data=algae,而应该先剔除水样中变量mnO2含有NA值才行。
- 所以,下一次的笔记是针对缺失值的处理的。
后记
本次博文是根据《数据挖掘与R语言(Luis Torgo著)》这本书的内容而写的笔记,本博文中所涉及的内容版权均归原作者所有。





